第一章——机器为何能够学习

   本系列是根据台大林轩田老师的《机器学习基石》中的课程内容整理及一些个人的理解与见解。如有错误之处，还请各位通过我的个人邮箱: 756161569@qq.com 联系我、批评指正，感谢！

机器学习是什么

介绍机器学习，我们还是从一个实际的例子开始说起吧。

大家都知道，银行在你申请信用卡的时候会收集你的个人信息，比如年龄、性别、收入、工作单位、工作性质、存款金额等等。然后根据这些信息来判断你这个人是好人还是坏人，并因此决策是否要发给你信用卡。

那银行是怎么根据这些信息做最终决策的呢？

简单来说，银行会根据在他资料库里过往所有人的信贷记录去判断你是个好人还是坏人。举个简单的例子，银行发现，年龄大于25岁，且存款额度大于50000元的人有着较好的信用表现。很幸运，你符合这样的条件，于是很开心的拿到了信用卡。

因此信用评估模型就是一个learning的问题，那么我们该如何使用历史数据做好learning呢？

机器学习架构

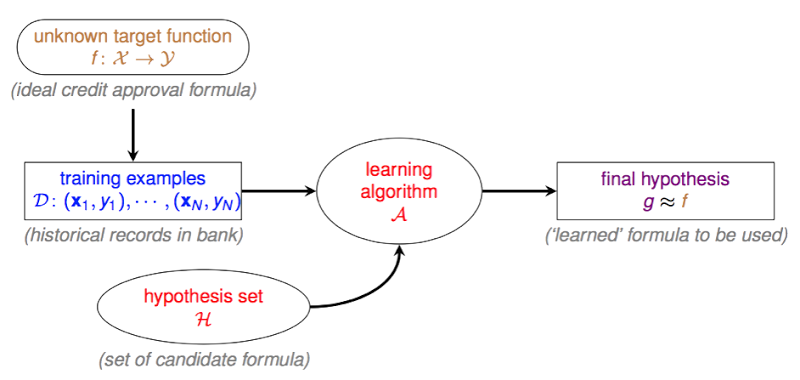
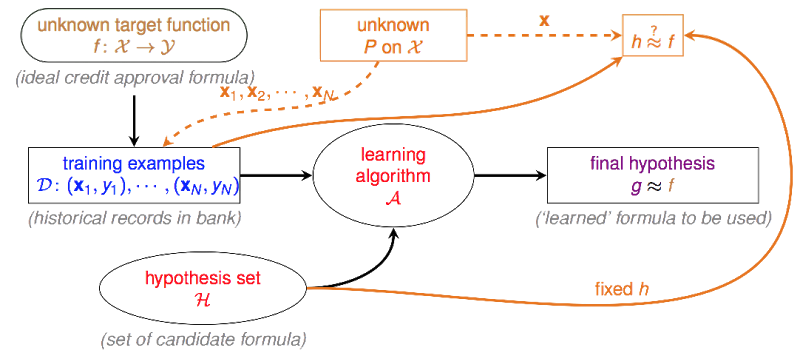
上图是林轩田老师给出的机器学习的基础架构，让我来一一介绍一下每个部分的意义。(基于上面银行卡决策场景)

• unknown target function

$$f = x \rightarrow y$$

其中x为输入参数，即信用卡发放判断中的用户数据，y是最终决策，即用户是好人还是坏人。f 就是从输入到输出的决策函数。

但正如名字所描述的，这个f是未知的，我们没有办法求出来，只能找一个与之接近的函数，达到近似的结果。

• D

  为训练数据集。即上文锁提到的，过往的信贷记录，包含用户多维度信息、是否有欺诈行为。

• H

一般称为hypothesis set。是一个由有限个或无限个方程组成的集合，算法A只能从H的范围内挑选方程。

• A

  Algorithm。即学习的算法，帮助我们在H中选择一个最接近f的函数。

• g

  final hypothesis set。即被A选出的最接近于f的函数。

机器学习真的可行吗

让我们先从一道初中数学题来分析这个问题吧。

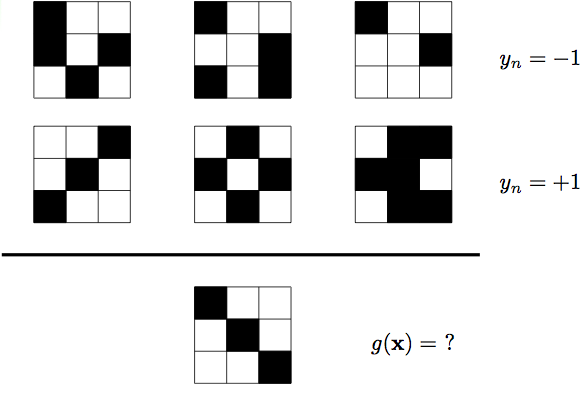
问题如上图所示，上面三个图y=-1,下面三个图y=+1。求最下面那个图的y值。

图片前两行可以理解为training set，对于第一行的所有样本，有f(x)=−1;对于第二行的所有样本，有f(x)=+1。

那么我们能不能通过这6笔数据来猜测一下f是长什么样的呢？

同学1和同学2利用各自的学习方法分别给出了自己的g。

同学1训练出来的g：
g1(对称图形)=+1
g1(非对称图形)=−1

同学2训练出来的g：
g2(左上角为白色的图形)=+1
g2(左上角为黑色的图形)=−1

对于training set中所有样本，有g1(x)=g2(x)=f(x)，即两个g1,g2与f的表现是一致的，似乎可以认为他们都”学”到了东西，但是对于测试样本来说g1(x)=+1,g2(x)=−1。

真实的f我们无法知道，如果他们中的某一个人在所有非训练的资料中也和f(x)表现一致，我们才能说他们当中某个人真的学到了东西。但在目前这种情况下，我们无法说同学1学到了东西还是同学2学到了东西。

霍夫丁不等式的证明

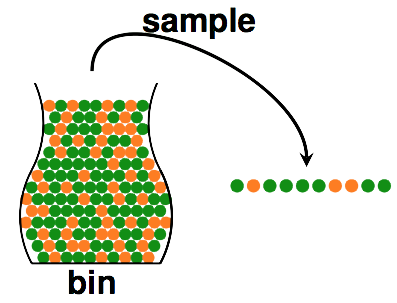
让我们以从一个罐子里取求的例子来解释这个概率的问题吧。

假设一个罐子里有1000个黄色的球和绿色的球，现在我们取出10个球，其中6个是黄色的球，4个是绿色的球。

那么，我们能认为这1000个球里有600个黄色的球么？答案是否定的，因为一次抽样带来的随机性会让测试样本与实际样本之间的差别不可预计。

但如果我们抽取更多次，比如我们放回的方式抽取了10000次，结果是P(红球)=0.6，那么我们就能大致确定罐子里有600个球了。因为测试次数越多，我们的测试样本与实际样本之间的差别会越来越小。

$$\mathbb{P}[|\nu-\mu|>\varepsilon] \leq 2exp(−2\varepsilon^{2}N)$$

上面的公式就是著名的霍夫丁不等式。其中 \(\nu\) 是我们测试样本的概率，\(\mu\) 是实际生产的概率，\(\varepsilon\)是容忍度，当\(\varepsilon\)非常小的时候，我们称 \(\nu\)与\(\mu\) 差不多(PAC, probably approximately correct)。

我们发现,只要让\(2exp(−2\varepsilon^{2}N)\)减小，就能让\(\nu\)与\(\mu\) 差别很大的概率上限非常小。该函数是一个指数函数，\(\varepsilon\)是一个常数，那么我们只需要让N(样本数量)变得很大，就能让\(\nu\)与\(\mu\)差不多。

有了上面的概率基础，我们再来看看今天的问题。

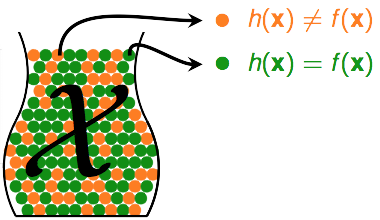
f(x)是我们的目标函数，h(x)是属于hypothesis set H的某一个方程。

• 如果h(x)≠f(x)，即他们判断不一致，我们记第n个小球是红色
• 如果h(x)=f(x)，即他们判断一致，我们记第n个小球是绿色

那么判断我们的hypothesis set是否正确的问题，就变成了一个概率的问题。所以，我们只要保证我们在测试样本上h(x)=f(x)，测试样本足够多。我们就能认为在生产上，对于没有看到的数据他很有可能相等。

机器学习的前提

我们知道h(x)≠f(x)的时候是计算函数的一次错误，我们定义\(E_{in}\)为测试样本上的错误概率(in-sample-error)。 \(E_{out}\)为总体样本上的错误概率(out-sample-error)。

那么对于h来说：

$$E_{out}(h)=\varepsilon[h(x)≠f(x)]$$ $$E_{in}(h)=\frac {1} {N}\sum_{i=1}^n[h(x)≠y_{n}]$$

上面一节我们刚刚用霍夫丁不等式证明了N很大时测试样本的概率与生产样本的概率”差不多”。也就是\(E_{in}\)和\(E_{out}\)存在一个上限，使用霍夫丁不等式表示即为:

$$\mathbb{P}[|E_{out}-E_{in}|>\varepsilon] \leq 2exp(−2\varepsilon^{2}N)$$

霍夫丁不等式告诉我们，在数量很大的情况下，测试数据集上的错误率会接近实际生产的错误率，这样我们就有了预测的前提。

上图就是说明了，当霍夫丁不等式上线“上界”足够小时，我们可以说h在sample中的表现(错误率)与h在总体中的表现是差不多的。

所以理论上，我们只需要在训练数据集很大的情况下选择一个\(E_{in}\)很小h，我们就可以说，我们选择的这个h的 \(E_{out}\) 也很小，也就是说我们学到了！

总结

我们回到文章最开始提到的，我们怎么去判断一个人是否可以发放信用卡呢？相信大家现在应该有一点思路了。

我们选择过去的信用记录作为训练样本，我们选择一个在过去训练样本中出错最少的h作为g(\(E_{in}\)) 最小)，霍夫丁不等式告诉我们在总体的样本中的错误率会和训练样本中的”差不多”。

有了这样的前提，我们就可以说，我们能通过过去，预测未来！