第二章——PLA演算法

   本系列是根据台大林轩田老师的《机器学习基石》中的课程内容整理及一些个人的理解与见解。如有错误之处，还请各位通过我的个人邮箱: 756161569@qq.com 联系我、批评指正，感谢！

上一章，我们根据霍夫丁不等式，从概率论的角度证明了机器学习是可行的。今天我们就要做的就是介绍一个简单的机器学习算法——Perceptron Learning Algorithm。

感知器

在介绍第一个机器学习算法前，我们需要先介绍一个感知器。

感知器是使用特征向量来表示一种演算法，是一种二元分类器，把矩阵上的输入 x（实数值向量）映射到输出值 f(x)上（一个二元的值）。

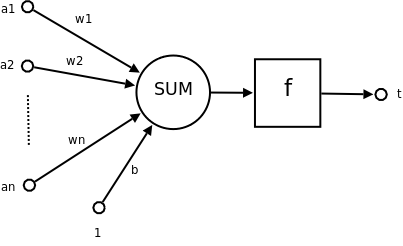
如图所示，\(a_{1}\) ~ \(a_{n}\) 是n维输入向量的各个分量，而W则是各个分量在最终决策上的权重.b是偏置，一个不依赖于任何输入值的常数,偏置可以认为是激励函数的偏移量。

使用数学函数表达式表示即为:

$$t=f(\sum_{i=1}^n w_{i}x_{i}+b)=f(W^{T}*X)$$

二元分类一般公式

令h(x)是一个perceptron，你给我一个X(X是一个特征向量)，把X输入h(x)，它就会输出这个x的类别。譬如在信用违约风险预测当中，输出就可能是这个人会违约，或者不会违约。

本质上讲，perceptron是一种二元线性分类器，它通过对特征向量的加权求和，并把这个”和”与事先设定的门槛值(threshold)做比较，高于门槛值的输出1，低于门槛值的输出-1。

$$f(x)= \begin{cases} 1, & \text {if \(W^{T}*X\)> threshold} \\ -1, & \text{else} \end{cases}$$

如果使用符号函数sign来表示就是:

$$h(x)=sign(\sum_{i=1}^n w_{i}x_{i}+b)$$

sign函数就是对x去正负号，如果x<0,输出-1，反之输出+1。

为了简化表示，我们令 \(w_{0}=1\),则b=\(w_{0}*b\)，所以上式可继续简化为:

$$h(x)=sign(\sum_{i=0}^n w_{i}x_{i})=W^{T}*X$$

看到这里，大家可能会被各种符号搞晕，所以在此特地解释一下，方便下文及以后的文章做公式。

• \(w_{i}\) ——小写的w加一个下标代表了一个向量中第i个的值。
• W ——大写的 W 代表向量。
• h(x)——代表以特征向量为入参的机器学习演算法。

Perceptron Learning Algorithm (PLA)

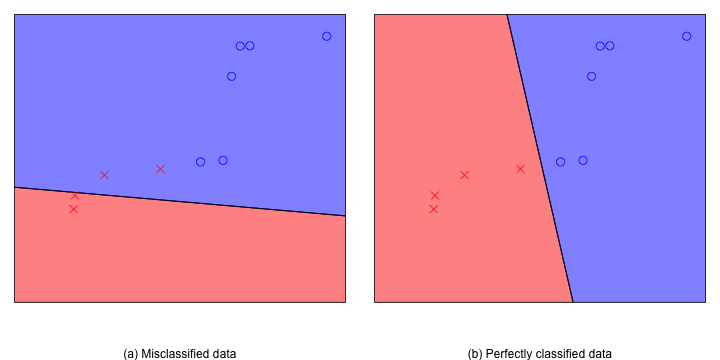
如图所示，在一个平面内有N个圈圈和叉叉，我们需要用一条直线将所有的圈圈和叉叉分开。

其实这个问题也类似于将好人和坏人分类，我们需要使用上面定义的f(x)函数，当圈圈输入时输出+1，当叉叉输入时，输出-1。

PLA演算法是如何做到的呢？

我们假定给定的数据是线性可分的，也就是肯定能找到一条直线将圈圈和叉叉完全分开。那么我们可以先随机给定一条直线，然后用所有的点去验证这条直线是否线性可分，一旦发生错误就将线旋转，直到这条线在所有数据集上都没有错误。

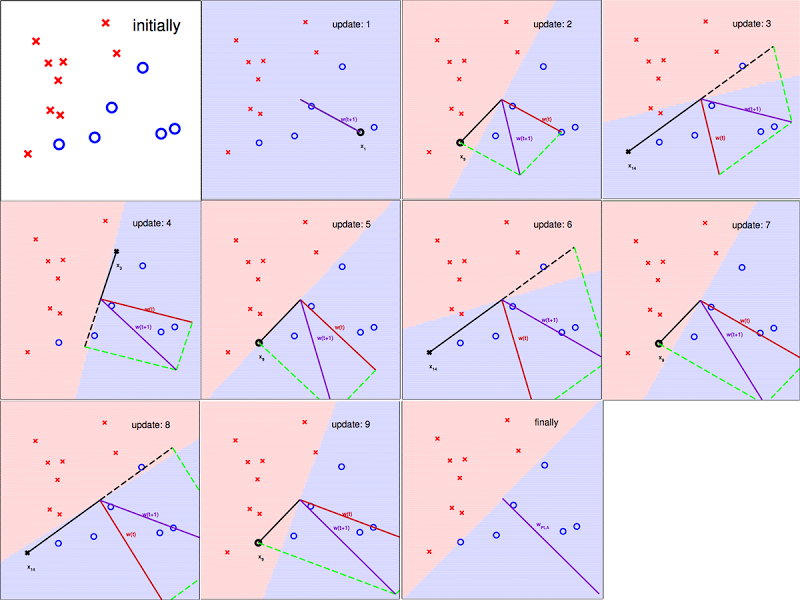
上图即为课程中林老师给出的更新过程，我们从第三张图片开始看吧，图中有一个圈圈被错误的分类成了叉叉，所以分类线忘该点的方向移动一步(第四张图片)可以将圈圈包含在圈圈的分类内。

但从第四张图片中我们也可以看出这次移动也导致了原先被成功分类的圈圈这次被错误分类了，所以每次移动以后，我们都必须用所有数据重新验证一次。当所有圈圈和叉叉都被正确分类的时候，我们就停下移动。(最后一张图)

PLA可行性证明

经过上面的讲解，大家应该都知道PLA是如何训练，将测试样本分类了。但细心的同学可能会提出一个问题，训练的算法是一个死循环，直到找不到错误才会停止，那么会不会永远也不会停止呢？或者换个问法，我们这样不停转，究竟能不能找到那条准确分类的线呢？

我们设我们的目标W为\(W_{f}\),第t次训练的W为\(W_{t}\)。

因为\(W_{f}\)是完美的，所以有以下性质(1):

$$y_{n(t)}W_{f}^{T}X_{n(t)} \geq min \; y_{n}W_{f}^{T}X_{n} > 0$$

当PLA发现错误，更新错误的时候，我们可以表示\(W_{t+1}\):

$$W_{t+1}=W_{t}+y_{n(t)}X_{n(t)}$$

注: 该公式的意义为，当PLA发现错误的时候，向出错的相反的方向更新W，
更新长度取决于出错样本。

因为\(W_{f}^{T}\) 是固定的，且大于0，所以我们将上式两边同时乘以\(W_{f}^{T}\)：

$$W_{f}^{T}*W_{t+1}=W_{f}^{T}*(W_{t}+y_{n(t)}X_{n(t)})$$

将右边展开,利用性质(2)可得:

$$W_{f}^{T}*W_{t+1}\geq W_{f}^{T}*W_{t}+ min \; y_{n}W_{f}^{T}X_{n}$$

所以:

$$W_{f}^{T}*W_{t+1} > W_{f}^{T}*W_{t}$$

由于W 与\(W_{f}\) 都是向量，我们只需要证明两个向量的夹角变小了，就能证明W越来越靠近我们目标的\(W_{f}\)。

上面我们证明了两个向量的乘积会变大，但导致向量乘积变大有两个因素——1.向量长度，2.向量夹角。

所以我们需要证明向量长度的增加是有限的，我们就能证明两个向量是在慢慢靠近的。

让我们来看一下每次移动，向量长度的变化:

$$||W_{t+1}||^{2} = ||W_{t}+y_{n(t)}X_{n(t)})||^{2}\\ ||W_{t+1}||^{2}=||W_{t}||^{2}+||y_{n(t)}X_{n(t)})||^{2}+2y_{n(t)}X_{n(t)}W_{t}^{T}$$

因为每次更新时，都表示预测与实际不符，所以\(2y_{n(t)}X_{n(t)}W_{t}^{T}\)<0

所以，上式又可以转化成下面不等式:

$$||W_{t+1}||^{2} \leq ||W_{t}||^{2}+||y_{n(t)}X_{n(t)})||^{2}$$

由于\(y_{n(t)}=\pm 1\),所以上式又可以精简成:

$$||W_{t+1}||^{2} \leq ||W_{t}||^{2}+max||X_{n(t)})||^{2}$$

所以，每次更新的最大长度即为样本参数向量的最大长度。

得出了每次更新W在长度增加方面的上限以后，我们再来看一下他们夹角余弦的变化范围

我们假设向量从\(W_{0}=0\)开始，经过T次错误更正，变为\(W_{T}\) 那么就有:

$$W_{f}^{T}W_{T} \geq W_{f}^{T}W_{T-1} + min \; y_{n(t)}X_{n(t)W_{f}^{T}}\\$$

使用递归的方式，将\(W_{T-1} 递归到 W_{0}\)最终可以得到:

$$W_{f}^{T}W_{T} \geq W_{f}^{T}W_{0} + T * min \; y_{n(t)}X_{n(t)W_{f}^{T}}\\$$

我们还可以得到:

$$||W_{T}||^{2} \leq ||W_{T-1}||^{2} + max||x_{n}||^{2}$$

还是用递归的方式，我们将\(W_{T}转化成W_{0}\)

$$||W_{T}||^{2} \leq ||W_{0}||^{2}+T*max||x_{n}||^{2}$$

有了这些基础，我们再来计算一下\(W_{f}和W_{T}\)的夹角余弦值:

$$\frac{W_{f}^{T}W_{T}}{||W_{f}||||W_{T}||} \geq \frac{T * min \; y_{n(t)}X_{n(t)W_{f}^{T}}}{||W_{f}||||W_{T}||} \geq \frac{T * min \; y_{n(t)}X_{n(t)W_{f}^{T}}}{||W_{f}||\sqrt{T}* \sqrt{max||x_{n}||^{2}}}$$

我们另:

$$\rho = min \; y_{n} \frac{W_{f}^{T}}{||W_{f}||^{2}}*X_{n} \\ R{2}=max ||X_{n}||^{2}$$

则，上式可以简化表示为：

$$\frac{T * min \; y_{n(t)}X_{n(t)W_{f}^{T}}}{||W_{f}||\sqrt{T}* \sqrt{max||x_{n}||^{2}}}= \frac{\sqrt{T}\rho}{R}$$

因为 \(\rho 和 R^{2}\)都是大于0的常数，余弦夹角小于等于1，所以： $\frac{\sqrt{T}\rho}{R} \leq 1 \\ T \leq \frac{R^{2}}{\rho^{2}}$

\(\rho 和 R^{2}\)都是大于0的常数。所以，T小于无穷大，也就是经过有限次迭代(T次)，最终找到\(W_{f}\);

最后总结

   综上所述，我们得到以下两个结论，也就是PLA的可行性证明。

• PLA能够帮助\(W_{T}\)越来越靠近\(W_{f}\)因为他们的夹角余弦值越来越小。
• 迭代次数T小于某个特定值，会在有限次迭代以后找到一条线能够把数据完美区分开。