神经网络训练的理论推导

学习一门新的知识，我更喜欢追根溯源，理解它背后的原理。

基础知识

1.矩阵计算

神经网络无论是训练还是预测都是基于矩阵运算，这样能大大降低训练、预测的时间。所以，关于矩阵计算相关的知识是必不可少的，如果在阅读过程中关于这部分有任何问题，都可以到矩阵运算及其规则以及Numpy官方文档 查阅。

2.梯度下降

神经网络训练的过程中是运用梯度下降的方式优化每个隐藏层节点的权重，所以，如果想要完全理解训练的整个过程，请先完成对梯度下降的理解。

神经网络的基本结构

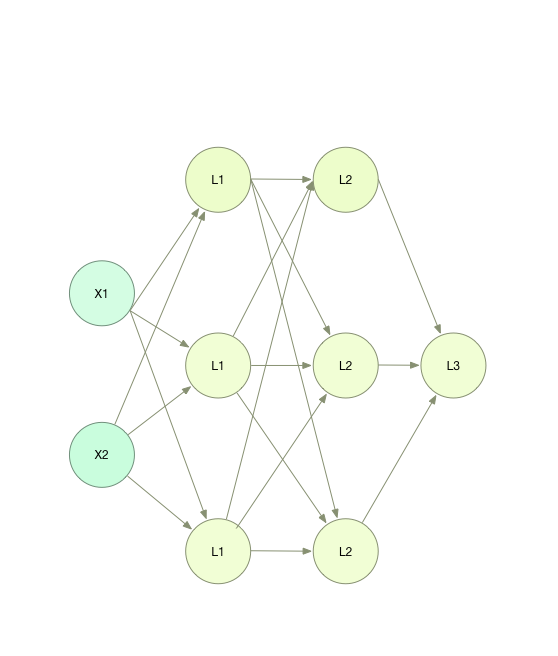
上图是一个非常简单的神经网络模型，其中每个圆点我们称作 神经元 。

图中最左边一列的X1、X2被称作 输入层 也就是最基本的输入数据。

第二、第三列被称作 隐藏层 。之所以被称作隐藏层，就是因为他们在整个模型的计算过程中虽然起着非常重要的作用，但我们并不能看到他们的结果，或者说他们的结果对我们来说是没有多少意义的。理论是，隐藏层是可以无限多的。

最后一列只有一个原点，被称作 输出层 (当然输出层也可以是多个输出节点)。顾名思义，他就是我们模型的计算结果。

神经网络的基本运算

大家可以注意到，每一层和下一层之间都会有一条直线连接，我们可以把直线理解为数据的输入，神经元理解为计算单元。所以，每一层的神经元计算都是利用上一层的计算结果，计算完成以后再将结果传递给下一层，直到最终结果的输出。

神经元的运算包括两步，第一步是一个简单的线性计算，我们可以先用最简单的线性运算: \(y = k*x+b\) 去表达。

线性计算完成以后，我们还需要对计算的结果做一次非线性的转换，也就是第二步运算，这种转换被称为 激活函数 。我们暂时使用最简单的非线性函数sigmoid去作为激活函数。

正是因为激活函数的存在，才让神经网络可以作为非线性可分数据的分类器。 至于为什么需要激活函数，以及激活函数为何一定得是非线性的，我们会在以后介绍。

所以每个神经的计算可以概括为:

$$Z=W*X+b$$ $$A=sigmoid(Z)$$

Forword Propagate (正向传播)

有了上面两步的介绍，就可以正式开始介绍整个神经网络计算的过程了。

因为第一列(第0层)是输入层，所以我们不做运算，我们从第1层开始，第一层的运算直接使用第0层的输出，所以我们可以表达为:

$$Z^1=W^1*X+b^1$$ $$A^1=sigmoid(Z^1)$$

上面公式中的上标1表示是第一层的运算参数。每一层的W和b都需要在训练之前初始化好，然后在训练的过程中不断更正，具体会在下面 反向传播 中介绍。

以此类推，第二层的计算就是:

$$Z^2=W^2*A^1+b^2$$ $$A^2=sigmoid(Z^2)$$

所以，总结下来，整个计算的公式可以概括为:

$$Z^n=W^n*A^{n-1}+b^n$$ $$A^n=sigmoid(Z^n)$$ $$其中A^0=X$$

矩阵与损失函数

上文锁提到的所有运算法则都是基于矩阵去运算的。例如，样本1是(x1=1,x2=2);样本2是(x1=3,x2=4)。假设我们的训练集就只有这两个样本，那么我们的输入矩阵X就可以表示为:

$$X=\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}$$

没错，我们就是将所有训练样本一次性全部放入一个矩阵中，借此来提高整个训练的速度。

大家应该可以从矩阵的形状观察出来，矩阵的每一列代表了一组训练样本。所以如果X的shape是(m,n)就代表了: 训练样本有m个，每个样本有n个维度。

所以，相应的，\(W^1\) 的shape就是(n,1)。因为无论有多少个训练样本都不会影响我们权重矩阵，权重矩阵只与样本维度有关。以矩阵表示就是(权重的数值为我们假设的值):

$$W^1=\begin{bmatrix} 1 \\ 3 \\ \end{bmatrix}$$

计算公式中的 b 被我们理解为偏移量。这个不难理解，它避免了我们的线性函数使用经过原点。

由矩阵的运算法则可知，b的shape应该等于X的行和W的列:

$$b=\begin{bmatrix} 2 \\ 2 \\ \end{bmatrix}$$

所以，正向传播中的计算都是基于上面对数据的矩阵表达来进行的。

经过一整套矩阵运算以后，我们最终可以得到最终的预测结果P。如果你之前接触过梯度下降，那么你一定猜到了下面应该怎么做。

没错，就是根据预测结果A和真实的结果Y之间的误差,反过来更新W和b。当然了，这是反向传播做的事情，我们在这一步先定义一个损失函数用来表达真实值与预测值之间的误差程度。

$$L=-\frac{1}{n} \sum_{i=1}^n y^i*log(a^i)+(1-y)*log(1-a^i)$$

反向传播

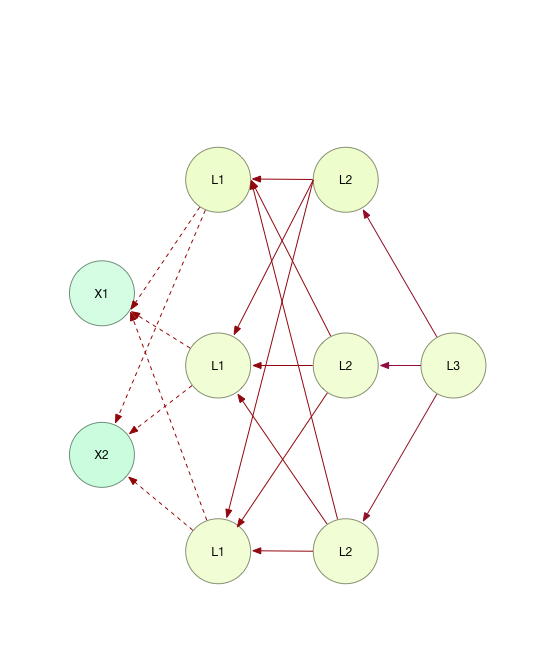
先放一张反向传播的示意图，图中红线部分就是由计算记过反向更新权重矩阵的路径(为了清晰表达，1.1中正向传播的线已经去掉)。

从图中可以清晰看出，每一层都是由上一层的反馈结果去更新，其中虚线部分标出的是输入参数，由于权重更新没有意义，所以以虚线表达，在实际计算中也不会更新。

每次更新的公式可以表达为:

$$W = W - \alpha \frac{\partial L}{\partial W}$$ $$b = b - \alpha \frac{\partial L}{\partial b}$$

以下是详细求导过程，对求导部分较为熟悉的读者可以忽略。 $\color {#red} {--------update \quad value \quad for \quad W----------}$

$$\frac{\partial L}{\partial W}=\frac{\partial L}{\partial A}*\frac{\partial A}{\partial Z}*\frac{\partial Z}{\partial W}$$ $$\frac{\partial L}{\partial W}=\frac{1}{n}(-\frac{Y}{A}+\frac{1-Y}{1-A})*(A(1-A))*X$$ $$\frac{\partial L}{\partial W}=\frac{1}{n}(A-Y)*X$$ $$\color {#red} {--------update \quad value \quad for \quad b----------}$$ $$\frac{\partial L}{\partial b}=\frac{\partial L}{\partial A}*\frac{\partial A}{\partial Z}*\frac{\partial Z}{\partial b}$$ $$\frac{\partial L}{\partial b}=\frac{1}{n}(-\frac{Y}{A}+\frac{1-Y}{1-A})*(A(1-A))*1$$ $$\frac{\partial L}{\partial b}=\frac{1}{n}(A-Y)$$

有了上面的推导公式，我们能就能从最后一个节点(第N层，也就是预测结果)以此递推更新W、b

我们仿照正向传播的形式，总结出以下递推式:

$$d_{w^{(n-1)}}=\frac{1}{n}(A^n-Y^n)*A^{(n-1)}$$ $$d_{b^{(n-1)}}=\frac{1}{n}(A^n-Y^n)$$

所以，我们只要按照这样的规律，遍历整个神经网络的深度，就可以得到每一层的权重，也就完成了训练。整个伪代码总结如下:

$$\color {#red} {for \quad i \quad from \quad n-1 \quad to \quad 1:}$$ $$W^i=W^i- \alpha * \frac{1}{n}(A^{i+1}-Y^{i+1})*A^{(i)}$$ $$b^i=b^i- \alpha * \frac{1}{n}(A^{i+1}-Y^{i+1})$$